Walkthrough
-
“Fit” walkthrough – Circle packing, noise fields, and Joe Jackson
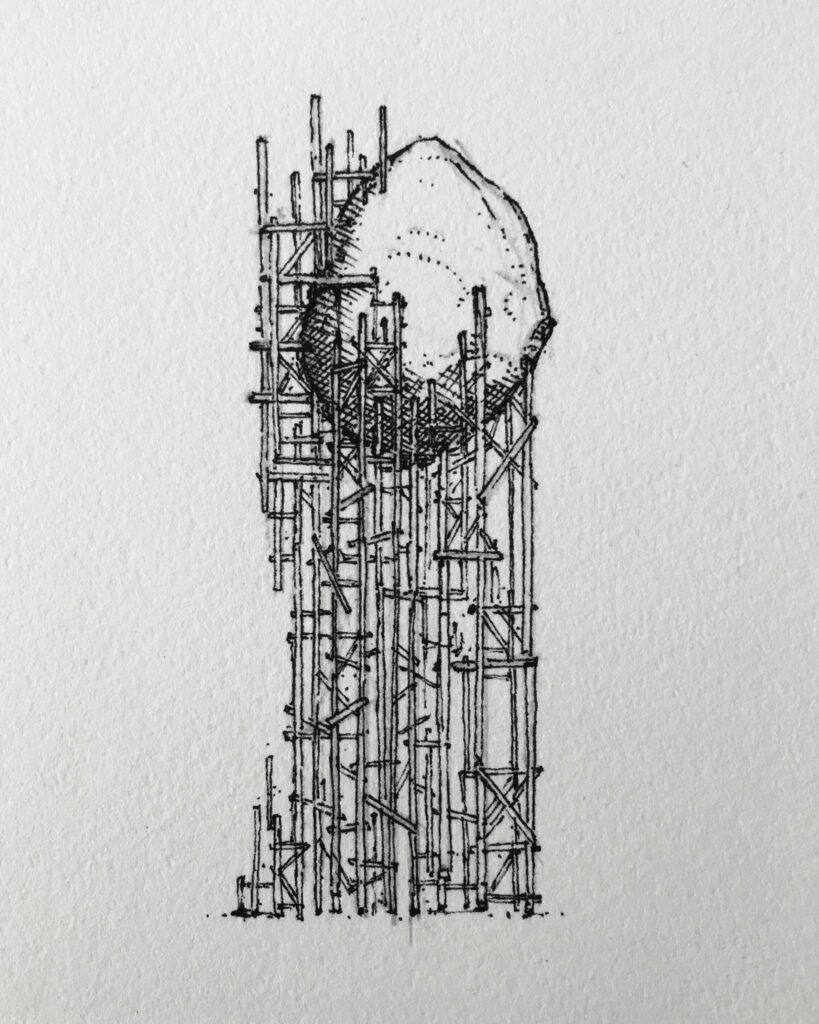
My new project “Fit” is minting as a free open edition on Base, for the entire month of June 204. Get yours here. As I was listening to Joe Jackson’s song “Fit”, the line “Square pegs in square holes” hit home and gave me the idea to ‘fit’ square shapes on a canvas in a […] Read more
-
Mining Structures walkthrough
Laxraven and I just released our collaborative project “Mining Structures” on FxHash. It was a huge success, and I have received many questions about the process and techniques used. Here is a quick walkthrough. The project started with a failure. @Laxraven had posted a beautiful architectural drawing on Twitter, and someone mentioned they would love […] Read more
-
Ammonites walkthrough
Following the unexpected success of the Ammonites NFT on fxhash, several people have asked me to give more information about my approach for producing this type of generative pieces. So here it is, I’m going to take this image and deconstruct it for you, step by step. 1. The easy part first – the background […] Read more